EDIT: Benchmarks are hard, or at least too hard for me. squeek502 on the Zig discord pointed out that the get part of my benchmark was being optimised away, which exaggerates the improvements we found. Thanks squeek for finding this! See addendum for more.
Ever implemented a balanced binary tree? Me neither, seems a pain! Red-Black, AVL, rotation, uncles/aunts, balance factors, sub-trees - that's a lot to keep track of. Luckily the world of computer science has a data structure that is far easier to implement and has similar properties: the skiplist.
I think I first learnt about skiplists at a Computer Science taster lecture about a decade ago at some university I was thinking of applying to. Clearly - given I gave them no further thought and I did not go to study there - the lecture wasn't that great. It is only recently since I became interested in how databases work that I met them again. They are often used in Log Structured Merge (LSM) trees as the datastructure for the memtable. The memtable holds the most recent data and needs to be quick to insert to and quick to read from.
So what is a skiplist? It is made up of levels, each of which is a linked list. At the bottom level the linked list has all your data in. The layer above has half the data in and the layer above has half of that, and so on. If a piece of data is on one level it most be on all the ones below it as well, and we link these together to let us descend the structure. A diagram is probably easiest.
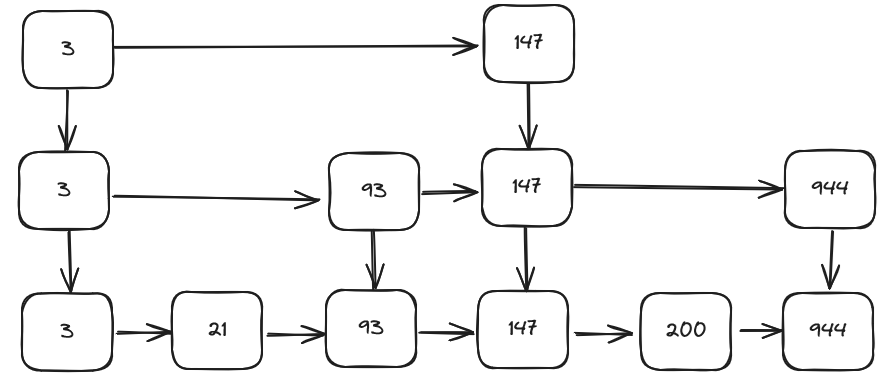
The property where each level has less and less data in it allows you to use it like a binary search tree. Each layer allows you to skip lots of data that you know is less than what you are looking for. Once you find something greater you descend to the next level which lets you do a more granular search.
If we were searching for 200 we would start at the 3 at the top and see that 200 > 3, so move to the next node, 147. Again, 200 > 147 but there is no next node on this level so we descend. At this level we do have a next node but its value is greater, so we know that the value will be between these two points. We again descend 147 and now the next node is the value we were looking for.
To build a skiplist you first descend the structure as you do for a lookup to find the node on the bottom level that should be before the new value. The first step is easy - a linked list insert. You then flip a coin, if it is heads then you also insert it on the level above. You keep flipping this coin until you get a tails or you create a new level. When this happens you need to make sure the head (the leftmost node) is on this new level so you can use it.
Implementation
This is pretty easy to implement but just to give you a rough idea here is some code in Zig. First off we define the types:
pub fn SkipList(comptime T: type) type {
return struct {
gpa: std.mem.Allocator,
rng: std.Random,
lt: *const CmpFn,
max_levels: usize,
levels: usize = 0,
head: ?*Node = null,
const CmpFn = fn (a: T, b: T) bool;
const Node = struct {
value: T,
next: ?*Node,
down: ?*Node,
};
};
}
I've decided here to build a generic one so we need a function that takes the value type and returns the skiplist type. We keep around an allocator in order to create nodes, a comparison function, the current number of levels, a pointer to the first node on the highest level and a random number generator. We also cap the total number of levels - more on why later. A node is then just a value and a pointer to the right and a pointer down.
There are two main parts of the algorithm: descending and then ascending to insert. First the descent:
/// Descends to the node before `v` if it exists, or to the node before where `v` should be inserted.
fn descend(self: *Self, v: T, levels: []*Node) *Node {
std.debug.assert(self.head != null);
std.debug.assert(self.lt(self.head.?.value, v));
var level = self.levels - 1;
var current = self.head.?;
while (true) {
const next = current.next;
const next_is_greater_or_end = next == null or self.lt(v, next.?.value);
if (!next_is_greater_or_end) {
current = next.?;
continue;
}
// If the `next` value is greater then `v` lies between `current` and `next`. If we are
// not at the base we descend, otherwise we are at the insertion point and can return.
if (next_is_greater_or_end and level > 0) {
levels[level] = current;
level -= 1;
current = current.down.?;
continue;
}
return current;
}
}
We start off with asserting some pre-conditions. In this case they are to make sure the caller has handled the edge cases so we don't muddy the function doing it, but even obvious "is this data reasonable?" assertions have helped me catch problems in the past. The code itself keeps moving right until we find a node whose next pointer is either null or greater than the value we're looking for. At this point we descend and continue travelling rightwards. Once we are at the bottom and find either the end or a greater value we can return the node.
The one other thing this function does is stash the nodes we follow down into the levels parameter. This will be useful for insert. A get is pretty self explanatory:
pub fn get(self: *Self, v: T, equal: *const CmpFn) ?*const T {
const head = self.head orelse return null;
if (equal(v, head.value)) return &head.value;
if (self.lt(v, head.value)) return null;
const levels = self.gpa.alloc(*Node, self.levels) catch unreachable;
defer self.gpa.free(levels);
const node = self.descend(v, levels);
if (equal(node.value, v)) return &node.value;
return null;
}
Note that we check whether the head is our value or greater than our value to satisfy the pre-conditions of descend.
An insert is a bit harder. First off we handle the cases where either the skiplist is empty or the value we are inserting is less than the head, so should be the head:
pub fn insert(self: *Self, v: T) !void {
var node = try self.gpa.create(Node);
errdefer self.gpa.destroy(node);
node.* = .{.next = null, .down = null, .value = v };
const head = self.head orelse {
self.head = node;
self.levels = 1;
return;
};
// If `v` is less than the head of the list we need to create a new node and make it the new
// head.
if (self.lt(v, head.value)) {
node.next = head;
var head_current: ?*Node = head.down;
var last = node;
for (0..self.levels - 1) |_| {
const new_node = try self.gpa.create(Node);
errdefer self.gpa.destroy(new_node);
new_node.* = .{ .next = head_current, .down = null, .value = v };
last.down = new_node;
head_current = head_current.?.down;
last = new_node;
}
self.head = node;
return;
}
When we make the new value the head we have to make sure that it is present on all levels, so we create a new node for every level, starting at the top.
const levels = try self.gpa.alloc(*Node, self.levels);
defer self.gpa.free(levels);
const prev = self.descend(v, levels);
const next = prev.next;
prev.next = node;
node.next = next;
const max_levels = @min(self.levels + 1, self.max_levels);
const random = self.rng.int(u32);
var down = node;
for (1..max_levels) |l| {
if (random & (@as(u32, 1) << @intCast(l)) == 0) break;
const new_node = try self.gpa.create(Node);
errdefer self.gpa.destroy(new_node);
new_node.* = .{ .next = null, .down = down, .value = v};
defer down = new_node;
if (l < self.levels) {
const above = levels[l];
new_node.next = above.next;
above.next = new_node;
continue;
}
// We've created a new level so we need to make sure head is at this level too.
self.levels += 1;
const new_head = try self.gpa.create(Node);
errdefer self.gpa.destroy(new_head);
new_head.* = .{ .down = self.head, .value = self.head.?.value, .next = new_node };
self.head = new_head;
return;
}
We use descend to get our insert position, and then insert our value in the bottom layer. We generate a random number and ascend, using individual bits from the random number to say whether we should insert at this level and continue, or stop. Using the bits is quicker than generating a random number at each level, and is why we cap the number of levels - we don't want to go over the width of the integer. The final edge case we need to handle is making sure the head has the same number of levels, if we create a new level.
Performance
So how does it perform? Using poop - think hyperfine but with some extra performance metrics and a more fun/childish (delete as appropriate) name - we can see it takes a couple of seconds to insert one million random 64bit integers and run get on one million more, when using sixteen levels:
> ../poop/zig-out/bin/poop './zig-out/bin/skiplist-perf pointers 16 1000000 1000000'
Benchmark 1 (3 runs): ./zig-out/bin/skiplist-perf pointers 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.01s ± 68.3ms 1.93s … 2.06s 0 ( 0%) 0%
peak_rss 65.4MB ± 64.3KB 65.3MB … 65.4MB 0 ( 0%) 0%
cpu_cycles 8.16G ± 288M 7.83G … 8.36G 0 ( 0%) 0%
instructions 2.40G ± 89.4 2.40G … 2.40G 0 ( 0%) 0%
cache_references 422M ± 22.3M 397M … 435M 0 ( 0%) 0%
cache_misses 198M ± 2.39M 196M … 200M 0 ( 0%) 0%
branch_misses 30.3M ± 17.8K 30.3M … 30.3M 0 ( 0%) 0%
The bulk of the time (90%) is spent in descend. The code here feels pretty simple but, after reading Data-Oriented Design, I'm suspicious that it is not very cache friendly: whenever we want to go right or down we need to chase a pointer.
Change 1: Dynamic Array
We should be able to fix that pretty easily for going down. Rather than storing a pointer down to another node, why don't we store a list of pointers? Each element in the list corresponds to a pointer on a given level:
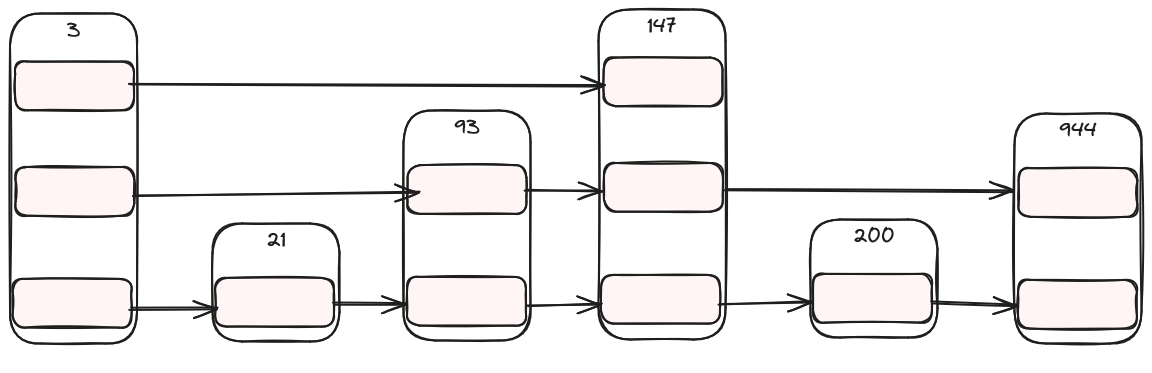
Implementing this needs only minor changes. Our nodes now look like the following, and the methods just need a little bit of tweaking to iterate through the list rather than following pointers:
const Node = struct {
value: T,
nexts: std.ArrayListUnmanaged(?*Node),
};
If we run our test binary:
> ../poop/zig-out/bin/poop './zig-out/bin/skiplist-perf pointers 16 1000000 1000000' './zig-out/bin/skiplist-perf dynamic 16 1000000 1000000'
Benchmark 1 (3 runs): ./zig-out/bin/skiplist-perf pointers 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.01s ± 68.3ms 1.93s … 2.06s 0 ( 0%) 0%
peak_rss 65.4MB ± 64.3KB 65.3MB … 65.4MB 0 ( 0%) 0%
cpu_cycles 8.16G ± 288M 7.83G … 8.36G 0 ( 0%) 0%
instructions 2.40G ± 89.4 2.40G … 2.40G 0 ( 0%) 0%
cache_references 422M ± 22.3M 397M … 435M 0 ( 0%) 0%
cache_misses 198M ± 2.39M 196M … 200M 0 ( 0%) 0%
branch_misses 30.3M ± 17.8K 30.3M … 30.3M 0 ( 0%) 0%
Benchmark 2 (3 runs): ./zig-out/bin/skiplist-perf dynamic 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.40s ± 9.42ms 2.39s … 2.41s 0 ( 0%) 💩+ 19.4% ± 5.5%
peak_rss 130MB ± 11.8KB 130MB … 130MB 0 ( 0%) 💩+ 98.5% ± 0.2%
cpu_cycles 9.69G ± 36.4M 9.65G … 9.72G 0 ( 0%) 💩+ 18.8% ± 5.7%
instructions 2.62G ± 9.17 2.62G … 2.62G 0 ( 0%) 💩+ 9.1% ± 0.0%
cache_references 375M ± 967K 373M … 375M 0 ( 0%) ⚡- 11.3% ± 8.5%
cache_misses 186M ± 279K 186M … 186M 0 ( 0%) ⚡- 6.2% ± 1.9%
branch_misses 30.6M ± 1.92K 30.6M … 30.6M 0 ( 0%) + 0.9% ± 0.1%
it's 20% worse?! We can at least see that our hunch about cache friendliness looks to be correct, that has improved, but overall this has not paid off in performance. Unfortunately I am not sure why this is as the same assembly instructions appear hot in both versions. If anyone has any theories I would love to hear them!
Interestingly the peak RSS also went up. Just storing pointers in the list seems like it should be more efficient then creating a node for every level where there is a pointer. I think this difference is probably from the list overallocating; when you append to a list and there is no space it needs to grow the underlying buffer by some multiplier. A common multiplier is 2x, which means in the worst case your list may take up twice as much memory as is being used.
So that was a bust, but I am not quitting yet. To lookup an item in Zig's ArrayList you first have to chase the pointer to the buffer and then index it - could we improve this?
Change 2: Static Array
Rather than having a separate array what if we stored the pointers in the node itself? Then when the node is loaded from memory it is likely we will get at least some of the pointers with it. To do that we will need to have a set number of levels, so we end up with something like this:
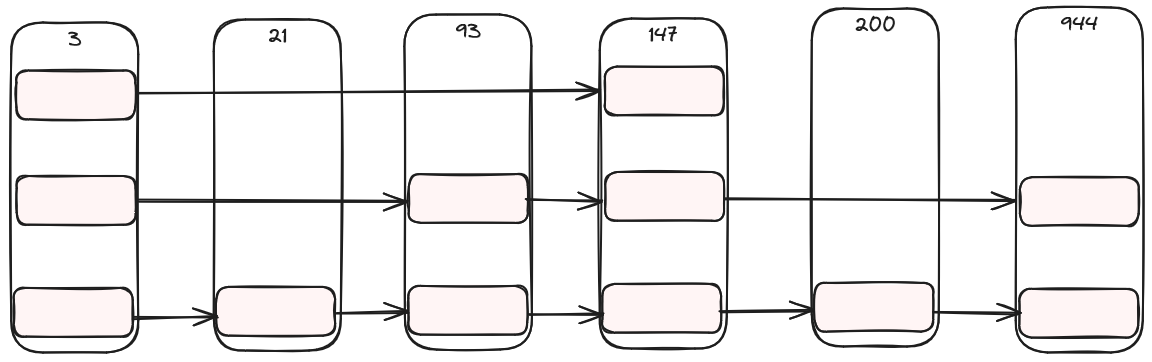
where each node has space for pointers for all the levels, but they are only used some of the time. Obviously this is quite wasteful of memory, but it is possible that it is worth it depending on your application. The Zig code for this uses a comptime integer to set the maximum number of levels:
pub fn SkipList(comptime N: usize, comptime T: type) type {
comptime {
std.debug.assert(N <= 32);
}
const Node = struct {
value: T,
nexts: [N]?*Node,
};
return struct {
// ...
};
}
This time we do get an improvement:
> ../poop/zig-out/bin/poop './zig-out/bin/skiplist-perf pointers 16 1000000 1000000' './zig-out/bin/skiplist-perf dynamic 16 1000000 1000000' './zig-out/bin/skiplist-perf static 16 1000000 1000000'
Benchmark 1 (3 runs): ./zig-out/bin/skiplist-perf pointers 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.01s ± 68.3ms 1.93s … 2.06s 0 ( 0%) 0%
peak_rss 65.4MB ± 64.3KB 65.3MB … 65.4MB 0 ( 0%) 0%
cpu_cycles 8.16G ± 288M 7.83G … 8.36G 0 ( 0%) 0%
instructions 2.40G ± 89.4 2.40G … 2.40G 0 ( 0%) 0%
cache_references 422M ± 22.3M 397M … 435M 0 ( 0%) 0%
cache_misses 198M ± 2.39M 196M … 200M 0 ( 0%) 0%
branch_misses 30.3M ± 17.8K 30.3M … 30.3M 0 ( 0%) 0%
Benchmark 2 (3 runs): ./zig-out/bin/skiplist-perf dynamic 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.40s ± 9.42ms 2.39s … 2.41s 0 ( 0%) 💩+ 19.4% ± 5.5%
peak_rss 130MB ± 11.8KB 130MB … 130MB 0 ( 0%) 💩+ 98.5% ± 0.2%
cpu_cycles 9.69G ± 36.4M 9.65G … 9.72G 0 ( 0%) 💩+ 18.8% ± 5.7%
instructions 2.62G ± 9.17 2.62G … 2.62G 0 ( 0%) 💩+ 9.1% ± 0.0%
cache_references 375M ± 967K 373M … 375M 0 ( 0%) ⚡- 11.3% ± 8.5%
cache_misses 186M ± 279K 186M … 186M 0 ( 0%) ⚡- 6.2% ± 1.9%
branch_misses 30.6M ± 1.92K 30.6M … 30.6M 0 ( 0%) + 0.9% ± 0.1%
Benchmark 3 (6 runs): ./zig-out/bin/skiplist-perf static 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 898ms ± 23.4ms 862ms … 925ms 0 ( 0%) ⚡- 55.3% ± 3.5%
peak_rss 145MB ± 11.3KB 145MB … 145MB 0 ( 0%) 💩+122.4% ± 0.1%
cpu_cycles 3.49G ± 93.8M 3.34G … 3.59G 0 ( 0%) ⚡- 57.3% ± 3.5%
instructions 716M ± 19.4 716M … 716M 0 ( 0%) ⚡- 70.2% ± 0.0%
cache_references 113M ± 3.45M 108M … 116M 0 ( 0%) ⚡- 73.3% ± 4.9%
cache_misses 46.5M ± 190K 46.3M … 46.8M 0 ( 0%) ⚡- 76.6% ± 1.1%
branch_misses 15.5M ± 60.5K 15.4M … 15.6M 0 ( 0%) ⚡- 49.0% ± 0.3%
As expected our memory usage has gone up, although not that much more from the dynamic array. We are now much quicker however! I am sure more performance could be eeked out here. Perhaps we could try storing multiple values per-node at the expense of making inserts more complicated. Or maybe we could improve memory usage by deciding how many levels a node will be up front and storing only that many pointers. For now this post is long enough.
Addendum
As mentioned at the start of the post it turns out the results are being exaggerated because running get on 1000000 integers was being optimised away - thanks/curses LLVM! squeek provided the fix: use std.mem.doNotOptimizeAway on the return value. With that our results are more modest, but still in line with what we got previously:
> ../poop/zig-out/bin/poop './zig-out/bin/skiplist-perf pointers 16 1000000 1000000' './zig-out/bin/skiplist-perf static 16 1000000 1000000'
Benchmark 1 (3 runs): ./zig-out/bin/skiplist-perf pointers 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 3.57s ± 767ms 2.79s … 4.32s 0 ( 0%) 0%
peak_rss 65.4MB ± 61.8KB 65.3MB … 65.4MB 0 ( 0%) 0%
cpu_cycles 11.9G ± 1.19G 10.8G … 13.2G 0 ( 0%) 0%
instructions 2.40G ± 2.36K 2.40G … 2.40G 0 ( 0%) 0%
cache_references 463M ± 19.7M 451M … 486M 0 ( 0%) 0%
cache_misses 213M ± 7.10M 207M … 221M 0 ( 0%) 0%
branch_misses 30.6M ± 472K 30.1M … 31.1M 0 ( 0%) 0%
Benchmark 2 (3 runs): ./zig-out/bin/skiplist-perf static 16 1000000 1000000
measurement mean ± σ min … max outliers delta
wall_time 2.17s ± 224ms 2.01s … 2.42s 0 ( 0%) ⚡- 39.3% ± 35.8%
peak_rss 145MB ± 27.3KB 145MB … 145MB 0 ( 0%) 💩+122.4% ± 0.2%
cpu_cycles 8.60G ± 793M 8.04G … 9.51G 0 ( 0%) ⚡- 27.9% ± 19.2%
instructions 1.11G ± 537 1.11G … 1.11G 0 ( 0%) ⚡- 53.7% ± 0.0%
cache_references 295M ± 20.3M 283M … 319M 0 ( 0%) ⚡- 36.2% ± 9.8%
cache_misses 133M ± 10.1M 127M … 145M 0 ( 0%) ⚡- 37.4% ± 9.3%
branch_misses 30.2M ± 521K 29.8M … 30.8M 0 ( 0%) - 1.4% ± 3.7%